Principal › Apuntes de Automática › CAPÍTULO 2

2.2 Lineal frente a no lineal

26 May, 2011 - 19:24 — joaquinm13
Versión para imprimirVersión para imprimir

Es importante tener muy presente los conceptos lineal y no lineal. La consideración de lineal para un modelo y las expresiones matemáticas que lo definen facilita mucho su manejo y comprensión. Sin embargo, teniendo en cuenta que, en general, los sistemas reales son no lineales, el grado de aproximación que se requiere para convertir un sistema no lineal en lineal siempre ha de ser tenido en cuenta. Como muestra, cuando en el ejemplo 2.1 se asume que el comportamiento del muelle es lineal, debemos tener en cuenta que esto exige, para que el modelo tenga suficiente precisión, que los esfuerzos aplicados sobre el muelle sean pequeños, lo cual ya nos está indicando que el modelo lineal deducido en el ejemplo no es válido para cualquier condición de funcionamiento.

Figura 2.4. Linealización a tramos

Linealizar un sistema no lineal es una técnica habitual que ayuda mucho en el análisis de los sistemas no lineales, sin embargo, nunca hay que perder de vista el ámbito de validez del modelo lineal y el error que se comete. Véase por ejemplo la Figura 2.4, donde la función no lineal 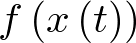$f\left( {x\left( t \right)} \right)$ ha sido linealizada a tramos en el entorno de diferentes puntos de operación (1 a 4). Esto se ha hecho así porque el error que se comete es mucho menor que si se linealiza la función en un solo tramo para todo el dominio de interés (segmento s).  Dicho esto, hay que tener en cuenta ahora que la función no lineal 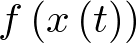$f\left( {x\left( t \right)} \right)$ podrá ser aproximada mediante 4 expresiones linealizadas, cada una de las cuales sólo será válida en su dominio correspondiente (entorno de los puntos 1 a 4); por tanto, dependiendo del tramo de operación, el modelo lineal a aplicar deberá ser el apropiado, ya que en caso contrario los errores cometidos podrían hacer inoperativo el modelo. Así por ejemplo, si el sistema no lineal va a trabajar en torno a un punto de operación (supongamos 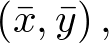$\left( {\bar x,\bar y} \right),$ punto 3 de la Figura 2.4) con pequeños desplazamientos alrededor de él, el modelo lineal a utilizar será el que describe dicho entorno, no siendo necesarios el resto de modelos por ser puntos de operación en los que no se va a encontrar el sistema.
Una técnica habitual de linealización de funciones no lineales consiste en realizar un desarrollo en serie de Taylor de la expresión no lineal alrededor de un punto de operación concreto. Así por ejemplo, si como en la Figura 2.4 se considera que el punto de operación normal es 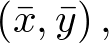$\left( {\bar x,\bar y} \right),$ la ecuación no lineal 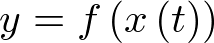$y = f\left( {x\left( t \right)} \right)$ puede ser desarrollada alrededor de ese punto del modo siguiente:

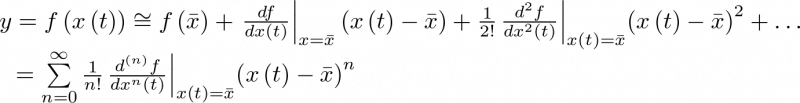$\begin{array}{l} y = f\left( {x\left( t \right)} \right) \cong f\left( {\bar x} \right) + {\left. {\frac{{df}}{{dx\left( t \right)}}} \right|_{x = \bar x}}\left( {x\left( t \right) - \bar x} \right) + \frac{1}{{2{\rm{!}}}}{\left. {\frac{{{d^2}f}}{{d{x^2}\left( t \right)}}} \right|_{x\left( t \right) = \bar x}}{\left( {x\left( t \right) - \bar x} \right)^2} + \ldots \\ \,\,\,\, = \sum\limits_{n = 0}^\infty {\frac{1}{{n{\rm{!}}}}} {\left. {\frac{{{d^{\left( n \right)}}f}}{{d{x^n}\left( t \right)}}} \right|_{x\left( t \right) = \bar x}}{\left( {x\left( t \right) - \bar x} \right)^n} \\ \end{array}$ (2.30)

Si la variación 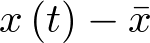$x\left( t \right) - \bar x$ es pequeña (validez de la aproximación de la curva mediante el segmento), los términos de orden superior en 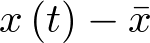$x\left( t \right) - \bar x$ pueden ser obviados, con lo cual la ecuación (2.30) puede ser escrita abreviadamente como

\[y\left( t \right) \simeq f\left( {\bar x} \right) + K\left( {x\left( t \right) - \bar x} \right);{\rm{ donde }}K = {\left. {\frac{{df}}{{dx\left( t \right)}}} \right|_{x\left( t \right) = \bar x}}\] (2.31)

Esto es, puesto que 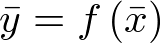 $\bar y = f\left( {\bar x} \right)$, la ecuación (2.31) puede ser escrita como

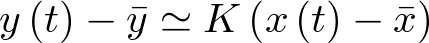$y\left( t \right) - \bar y \simeq K\left( {x\left( t \right) - \bar x} \right)$ (2.32)

Lo cual indica que 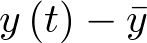$y\left( t \right) - \bar y$ es sensiblemente proporcional a 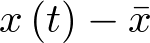$x\left( t \right) - \bar x$; esto es, (2.32) es un modelo lineal aproximado de 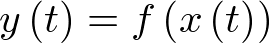$y\left( t \right) = f\left( {x\left( t \right)} \right)$ válido en el entorno 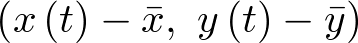$\left( {x\left( t \right) - \bar x,\,\,y\left( t \right) - \bar y} \right)$ del punto de operación.
Si f es una función de varias variables, supongamos dos por ejemplo8, el desarrollo en serie de Taylor de 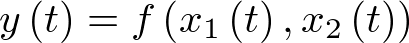$y\left( t \right) = f\left( {{x_1}\left( t \right),{x_2}\left( t \right)} \right)$ se escribiría, en el entorno de un punto de interés 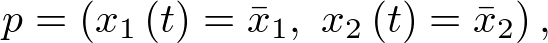$p = \left( {{x_1}\left( t \right) = {{\bar x}_1},\,\,{x_2}\left( t \right) = {{\bar x}_2}} \right),$ como

\[\begin{array}{*{20}{c}} {y\left( t \right) \cong f\left( {{x_1}\left( t \right),{x_2}\left( t \right)} \right) = f\left( {{{\bar x}_1},{{\bar x}_2}} \right) + \left[ {{{\left. {\frac{{\partial f}}{{\partial {x_1}\left( t \right)}}} \right|}_p}\left( {{x_1}\left( t \right) - {{\bar x}_1}} \right) + {{\left. {\frac{{\partial f}}{{\partial {x_2}\left( t \right)}}} \right|}_p}\left( {{x_2}\left( t \right) - {{\bar x}_2}} \right)} \right]} \hfill \\ { + \frac{1}{{2{\rm{!}}}}\left[ {{{\left. {\frac{{{\partial ^2}f}}{{\partial {x_1}^2\left( t \right)}}} \right|}_p}{{\left( {{x_1}\left( t \right) - {{\bar x}_1}} \right)}^2} + 2{{\left. {\frac{{{\partial ^2}f}}{{\partial {x_1}\left( t \right)\partial {x_2}\left( t \right)}}} \right|}_p}\left( {{x_1}\left( t \right) - {{\bar x}_1}} \right)\left( {{x_2}\left( t \right) - {{\bar x}_2}} \right) + {{\left. {\frac{{{\partial ^2}f}}{{\partial {x_2}^2\left( t \right)}}} \right|}_p}{{\left( {{x_2}\left( t \right) - {{\bar x}_2}} \right)}^2}} \right] + \cdots } \hfill \\ \end{array}\] (2.33)

Nuevamente, puesto que 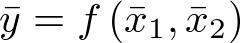 $\bar y = f\left( {{{\bar x}_1},{{\bar x}_2}} \right)$, la ecuación (2.33) puede ser escrita, despreciando los términos de orden superior, como un modelo matemático lineal válido alrededor del punto de operación p:

(2.34)

Ejemplo 2.5. Linealización de un modelo no lineal.  Sea la ecuación no lineal \[y = f\left( {{x_1},{x_2}} \right) = {x_1}{x_2}\]. Se trata de linealizarla en la región \[4 \le {x_1} \le 8{\rm{ y }}9 \le {x_2} \le 13.\] El punto lógico de operación para realizar la linealización es el medio en ambas regiones, esto es: \[{\bar x_1} = 6{\rm{ y }}{\bar x_2} = 11.\] Aplicando (2.34) se tiene que

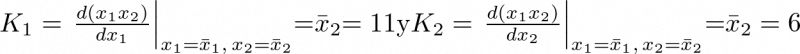${\rm{ }}{K_1} = {\left. {\frac{{d\left( {{x_1}{x_2}} \right)}}{{d{x_1}}}} \right|_{{x_1} = {{\bar x}_1},\,{x_2} = {{\bar x}_2}}}{\rm{ = }}{\bar x_2}{\rm{ = 11 y }}{K_2} = {\left. {\frac{{d\left( {{x_1}{x_2}} \right)}}{{d{x_2}}}} \right|_{{x_1} = {{\bar x}_1},\,{x_2} = {{\bar x}_2}}}{\rm{ = }}{\bar x_2} = 6$ (2.35)

La ecuación linealizada es pues

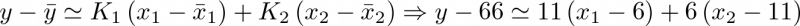$y - \bar y \simeq {K_1}\left( {{x_1} - {{\bar x}_1}} \right) + {K_2}\left( {{x_2} - {{\bar x}_2}} \right) \Rightarrow y - 66 \simeq 11\left( {{x_1} - 6} \right) + 6\left( {{x_2} - 11} \right)$ (2.36)

Donde 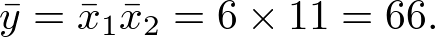$\bar y = {\bar x_1}{\bar x_2} = 6 \times 11 = 66.$ La ecuación (2.36) puede ser escrita también como

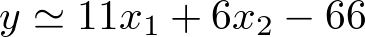$y \simeq 11{x_1} + 6{x_2} - 66$ (2.37)

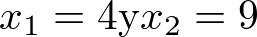Para ${x_1} = 4{\rm{ y }}{x_2} = 9$ por ejemplo, el valor verdadero de y es 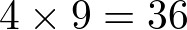$4 \times 9 = 36$. El valor linealizado se obtiene de (2.37) y vale 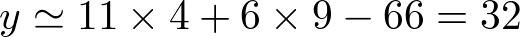$y \simeq 11 \times 4 + 6 \times 9 - 66 = 32$. Por tanto, en este punto el error cometido es de 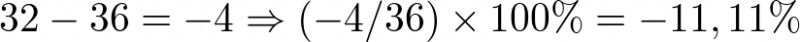$32 - 36 = - 4 \Rightarrow \left( {{{ - 4} \mathord{\left/ {\vphantom {{ - 4} {36}}} \right. \kern-\nulldelimiterspace} {36}}} \right) \times 100\% = - 11,11\%$. En el otro extremo, 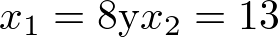${x_1} = 8{\rm{ y }}{x_2} = 13$,con lo cual el valor real de y es 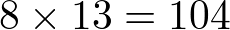$8 \times 13 = 104$, y el aproximado $y \simeq 11 \times 8 + 6 \times 13 - 66 = 100$. 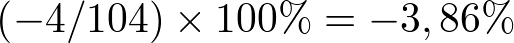Aquí el error es menor que en el otro extremo: $\left( {{{ - 4} \mathord{\left/ {\vphantom {{ - 4} {104}}} \right. \kern-\nulldelimiterspace} {104}}} \right) \times 100\% = - 3,86\%$.

En ingeniería de control es de gran interés la linealización de la ecuación de estado, ya que ello permite linealizar en torno a un punto el modelo de un sistema no lineal.  La ecuación de estado, como se sabe, es una función vectorial de varias variables, lo cual hace que su procedimiento de linealización sea un poco más complejo que el visto en esta sección. Trataremos esta cuestión con detalle en la sección 3.8 del capítulo siguiente.