Inicie su sesión para modificar los apuntes, usar los foros, etc. Si no es usuario de la web, regístrese.
2.4 Matriz de transición de estado y respuesta temporal
Desde el punto de vista del modelo de estado, una vez que se ha obtenido éste interesa conocer la información que proporciona, esto es, la posibilidad de analizar el comportamiento dinámico del sistema a lo largo del tiempo. Para ello se debe tener una expresión explícita de la solución o trayectoria del sistema en su espacio de estado, esto es, del vector de estado. Esta solución exige el cálculo de la ecuación de estado. Cuando ésta es no lineal, su solución puede ser muy compleja, de modo que la mayoría de las veces habrá que descartar la obtención de una expresión analítica, quedando pues la solución en el ámbito del análisis numérico realizado mediante computador. Sin embargo, cuando la ecuación de estado es lineal, bien porque el sistema lo es, o bien porque es el resultado de la linealización de un sistema no lineal, la ecuación de estado admite una solución analítica que es fácil de obtener y proporciona una información muy rica de la evolución temporal de las trayectorias (coordenadas del vector de estado) del sistema.
Sea pues la ecuación de estado en su forma lineal siguiente:
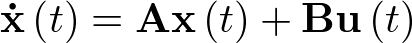 |
(2.65) |
Aplicando la transformada de Laplace con la condición inicial 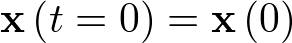 se tiene que
se tiene que
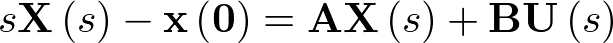 |
(2.66) |
O también
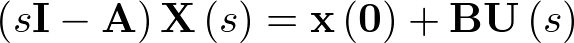 |
(2.67) |
Esto es,
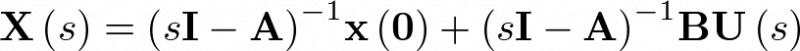 |
(2.68) |
Como se sabe, 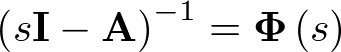 por tanto,
por tanto,
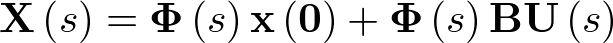 |
(2.69) |
Aplicando la transformada inversa de Laplace para obtener la solución temporal se tiene que
![${\bf{x}}\left( t \right) = {L^{\,\, - 1}}\left[ {{\bf{\Phi }}\left( s \right)} \right]\,{\bf{x}}\left( {\bf{0}} \right) + {L^{\,\, - 1}}\left[ {{\bf{\Phi }}\left( s \right){\bf{BU}}\left( s \right)} \right]$](/antonio.barragan/files/archivos_usuarios/78/form2.4-8%282.70%29.png) |
(2.70) |
La matriz
![${\bf{\Phi }}\left( t \right) = {L^{\,\, - 1}}\left[ {{\bf{\Phi }}\left( s \right)} \right]\,$](/antonio.barragan/files/archivos_usuarios/78/form2.4-9%282.71%29.png) |
(2.71) |
se denomina matriz de transición de estado. Nótese en la ecuación (2.70) como la matriz de transición de estado representa el paso del sistema desde el estado inicial 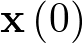 al considerado
al considerado 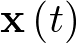 cuando la entrada es cero; esto es, describe la respuesta no forzada o natural del sistema.
cuando la entrada es cero; esto es, describe la respuesta no forzada o natural del sistema.
Teniendo en cuenta la operación de convolución16 en el dominio de la transformada de Laplace:
![$L\left[ {\int\limits_0^t {{f_1}\left( {t - \tau } \right){f_2}\left( \tau \right)d\tau } } \right] = {F_1}\left( s \right){F_2}\left( s \right);{\rm{ donde }}{F_1}\left( s \right) = L\left[ {{f_1}\left( t \right)} \right]{\rm{ y }}{F_2}\left( s \right) = L\left[ {{f_2}\left( t \right)} \right]$](/antonio.barragan/files/archivos_usuarios/78/form2.4-13%282.72%29.png) |
(2.72) |
Se tiene que la ecuación (2.70) puede ser escrita como
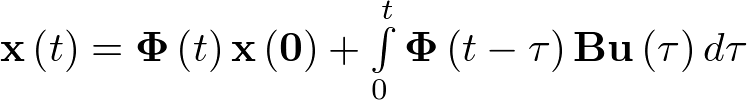 |
(2.73) |
Donde 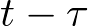 representa un adelanto en el tiempo de valor
representa un adelanto en el tiempo de valor 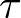 de la función
de la función 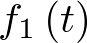 . La ecuación (2.73) es la solución de la ecuación diferencial de estado dada por (2.65). Evidentemente, si se conocen las condiciones iniciales
. La ecuación (2.73) es la solución de la ecuación diferencial de estado dada por (2.65). Evidentemente, si se conocen las condiciones iniciales 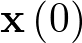 , la entrada
, la entrada 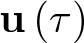 y la matriz de transición
y la matriz de transición 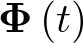 , puede calcularse numéricamente la solución de la ecuación de estado o respuesta temporal del vector de estado. Cuando el sistema no está forzado
, puede calcularse numéricamente la solución de la ecuación de estado o respuesta temporal del vector de estado. Cuando el sistema no está forzado 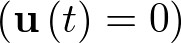 ésta es simplemente
ésta es simplemente
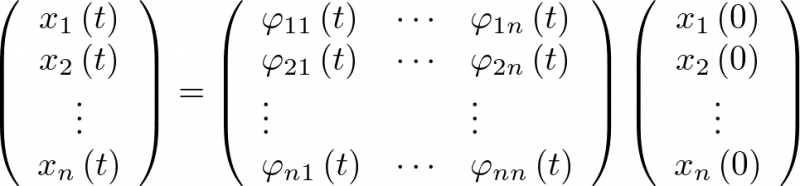 |
(2.74) |
Se puede comprobar fácilmente que la matriz de transición de estado 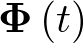 está dada por
está dada por
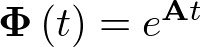 |
(2.75) |
Donde 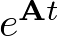 se denomina matriz exponencial. En efecto, supóngase que la entrada del sistema modelado por (2.65) es nula, con lo cual
se denomina matriz exponencial. En efecto, supóngase que la entrada del sistema modelado por (2.65) es nula, con lo cual
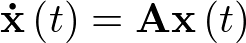 |
(2.76) |
Entonces, la solución de esta ecuación diferencial es, según (2.74),
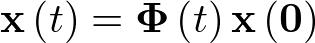 |
(2.77) |
Sustituyendo esta expresión en (2.76) se tiene que
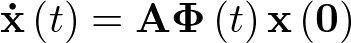 |
(2.78) |
Nótese que al derivar (2.77), el paso de esta ecuación a la (2.78) es inmediato si 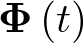 está dada por (2.75). Por tanto, la solución de la ecuación diferencial de estado puede ser escrita también como
está dada por (2.75). Por tanto, la solución de la ecuación diferencial de estado puede ser escrita también como
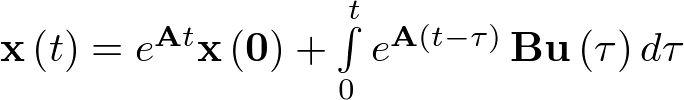 |
(2.79) |
Ejemplo 2.9. Respuesta temporal del sistema muelle – masa – amortiguador. Considérese que los valores de m, k y β del sistema de la figura 2.1 son tales que su ecuación de estado (2.7) está dada por
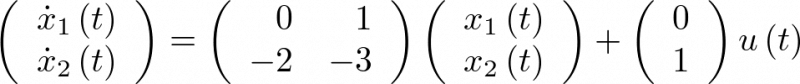 |
(2.80) |
Con objeto de evaluar la respuesta temporal del sistema se ha de calcular primero la matriz 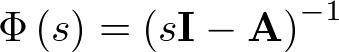 la cual se obtiene de la forma
la cual se obtiene de la forma
![\[\left( {s{\rm{I}} - {\rm{A}}} \right) = \left( {\left( {\begin{array}{*{20}{c}} s & 0 \\ 0 & s \\ \end{array}} \right) - \left( {\begin{array}{*{20}{c}} \hfill 0 & \hfill 1 \\ \hfill { - 2} & \hfill { - 3} \\ \end{array}} \right)} \right) = \left( {\begin{array}{*{20}{c}} s & { - 1} \\ 2 & {s + 3} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-34%282.81%29.png) |
(2.81) |
Por consiguiente,
![\[{\bf{\Phi }}\left( s \right) = {\left( {s{\rm{I}} - {\rm{A}}} \right)^{ - 1}} = \frac{1}{{\Delta \left( s \right)}}\left( {\begin{array}{*{20}{c}} {s + 3} & 1 \\ { - 2} & s \\ \end{array}} \right);{\rm{ donde }}\Delta \left( s \right) = \left| {\begin{array}{*{20}{c}} s & { - 1} \\ 2 & {s + 3} \\ \end{array}} \right| = {s^2} + 3s + 2 = \left( {s + 1} \right)\left( {s + 2} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-35%282.82%29.png) |
(2.82) |
Ahora, con objeto de obtener la descomposición en fracciones parciales se escribe
![\[{\bf{\Phi }}\left( s \right) = \left( {\begin{array}{*{20}{c}} {\frac{{s + 3}}{{\left( {s + 1} \right)\left( {s + 2} \right)}}} & {\frac{1}{{\left( {s + 1} \right)\left( {s + 2} \right)}}} \\ {\frac{{ - 2}}{{\left( {s + 1} \right)\left( {s + 2} \right)}}} & {\frac{s}{{\left( {s + 1} \right)\left( {s + 2} \right)}}} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\frac{A}{{s + 1}} + \frac{B}{{s + 2}}} & {\frac{C}{{s + 1}} + \frac{D}{{s + 2}}} \\ {\frac{E}{{s + 1}} + \frac{F}{{s + 2}}} & {\frac{G}{{s + 1}} + \frac{H}{{s + 2}}} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-36%282.83%29.png) |
(2.83) |
Operando como en el ejemplo 2.6 se tiene que
![\[{\bf{\Phi }}\left( s \right) = \left( {\begin{array}{*{20}{c}} {\frac{2}{{s + 1}} - \frac{1}{{s + 2}}} & {\frac{1}{{s + 1}} - \frac{1}{{s + 2}}} \\ { - \frac{2}{{s + 1}} + \frac{2}{{s + 2}}} & { - \frac{1}{{s + 1}} + \frac{2}{{s + 2}}} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-37%282.84%29.png) |
(2.84) |
Aplicando ahora la transformada inversa de Laplace,
![\[{\bf{\Phi }}\left( t \right) = {e^{{\bf{A}}t}} = {L^{\,\, - 1}}\left[ {{\bf{\Phi }}\left( s \right)} \right]\, = \left( {\begin{array}{*{20}{c}} {2{e^{ - t}} - {e^{ - 2t}}} & {{e^{ - t}} - {e^{ - 2t}}} \\ { - 2{e^{ - t}} + 2{e^{ - 2t}}} & { - {e^{ - t}} + 2{e^{ - 2t}}} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-38%282.85%29.png) |
(2.85) |
Una vez calculada la matriz de transición de estado, la respuesta temporal del sistema para diferentes condiciones iniciales y señales de entrada puede calcularse mediante la ecuación (2.73). Por ejemplo, cuando ![\[{x_1}\left( 0 \right) = {x_2}\left( 0 \right) = 1{\rm{ y }}u\left( t \right) = 0\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-39.png) se tiene que
se tiene que
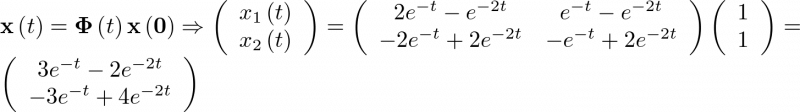 |
(2.86) |
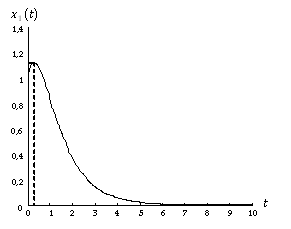
El la figura 2.9 se muestra la evolución temporal del vector de estado para las condiciones iniciales dadas. Nótese que aunque la velocidad 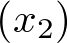 empieza a decrecer enseguida, hasta que no se hace cero, la masa (ver Figura 2.1) no para de moverse hacia abajo, con lo cual
empieza a decrecer enseguida, hasta que no se hace cero, la masa (ver Figura 2.1) no para de moverse hacia abajo, con lo cual 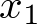 crece en este intervalo. En la Figura 2.10 se muestra la trayectoria del vector de estado en el espacio de estado del sistema (plano
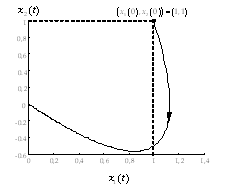
crece en este intervalo. En la Figura 2.10 se muestra la trayectoria del vector de estado en el espacio de estado del sistema (plano 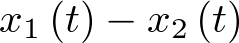 ). Esta representación se denomina retrato de fase. Nótese como el vector de estado, conforme el sistema va perdiendo la energía del estado inicial, tiende al punto (0,0) que es el punto de equilibrio o estado de mínima energía. El retrato de fase y el concepto de punto de equilibrio serán tratados en profundidad en el capítulo siguiente.
). Esta representación se denomina retrato de fase. Nótese como el vector de estado, conforme el sistema va perdiendo la energía del estado inicial, tiende al punto (0,0) que es el punto de equilibrio o estado de mínima energía. El retrato de fase y el concepto de punto de equilibrio serán tratados en profundidad en el capítulo siguiente.
 |
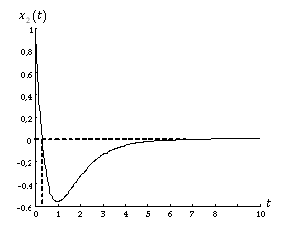 |
Figura 2.9. Respuesta temporal de las variables de estado para ![\[{x_1}\left( 0 \right) = {x_2}\left( 0 \right) = 1{\rm{ y }}u\left( t \right) = 0.\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-44.png) |
|
 |
|
| Figura 2.10. Trayectoria del vector de estado en el espacio de estado | |
Considérese ahora que el sistema está forzado, esto es, 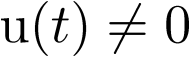 . Sea por ejemplo
. Sea por ejemplo 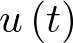 la función escalón unitario,
la función escalón unitario, 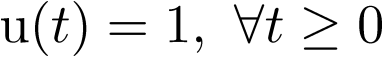 . En este caso, la ecuación (2.73) ha de ser usada en toda su extensión, utilizando el valor ya calculado de la matriz de transición
. En este caso, la ecuación (2.73) ha de ser usada en toda su extensión, utilizando el valor ya calculado de la matriz de transición  .
.
![\[{\bf{x}}\left( t \right) = \left( {\begin{array}{*{20}{c}} {2{e^{ - t}} - {e^{ - 2t}}} & {{e^{ - t}} - {e^{ - 2t}}} \\ { - 2{e^{ - t}} + 2{e^{ - 2t}}} & { - {e^{ - t}} + 2{e^{ - 2t}}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( 0 \right)} \\ {{x_2}\left( 0 \right)} \\ \end{array}} \right) + \int\limits_0^t {\,\left( {\begin{array}{*{20}{c}} {2{e^{ - \left( {t - \tau } \right)}} - {e^{ - 2\left( {t - \tau } \right)}}} & {{e^{ - \left( {t - \tau } \right)}} - {e^{ - 2\left( {t - \tau } \right)}}} \\ { - 2{e^{ - \left( {t - \tau } \right)}} + 2{e^{ - 2\left( {t - \tau } \right)}}} & { - {e^{ - \left( {t - \tau } \right)}} + 2{e^{ - 2\left( {t - \tau } \right)}}} \\ \end{array}} \right)} \left( {\begin{array}{*{20}{c}} 0 \\ 1 \\ \end{array}} \right)\left( 1 \right)d\tau \]](/antonio.barragan/files/archivos_usuarios/78/form2.4-51.png) |
(2.87) |
Después de operar con las matrices, el sumando que contiene la integral queda como
|
\[\begin{array}{l} \int\limits_0^t {\,\left( {\begin{array}{*{20}{c}} {{e^{ - \left( {t - \tau } \right)}} - {e^{ - 2\left( {t - \tau } \right)}}} \\ { - {e^{ - \left( {t - \tau } \right)}} + 2{e^{ - 2\left( {t - \tau } \right)}}} \\ \end{array}} \right)} d\tau = \left( {\begin{array}{*{20}{c}} {\int\limits_0^t {\left( {{e^{ - \left( {t - \tau } \right)}} - {e^{ - 2\left( {t - \tau } \right)}}} \right)} \,d\tau } \\ {\int\limits_0^t {\left( { - {e^{ - \left( {t - \tau } \right)}} + 2{e^{ - 2\left( {t - \tau } \right)}}} \right)} \,d\tau } \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{e^{ - t}}\int\limits_0^t {{e^\tau }d\tau - {e^{ - 2\tau }}\int\limits_0^t {{e^{2\tau }}d\tau } } } \\ { - {e^{ - t}}\int\limits_0^t {{e^\tau }d\tau + 2{e^{ - 2t}}\int\limits_0^t {{e^{2\tau }}d\tau } } } \\ \end{array}} \right) = \\ \left( {\begin{array}{*{20}{c}} {{e^{ - t}}\left[ {{e^\tau }} \right]_0^t - {\textstyle{1 \over 2}}{e^{ - 2\tau }}\left[ {{e^{2\tau }}} \right]_0^t} \\ { - {e^{ - t}}\left[ {{e^\tau }} \right]_0^t + {\textstyle{2 \over 2}}{e^{ - 2\tau }}\left[ {{e^{2\tau }}} \right]_0^t} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - {e^{ - t}} + {\textstyle{1 \over 2}}{e^{ - 2t}} + {\textstyle{1 \over 2}}} \\ {{e^{ - t}} - {e^{ - 2t}}} \\ \end{array}} \right) \\ \end{array}\] |
(2.88) |
 |
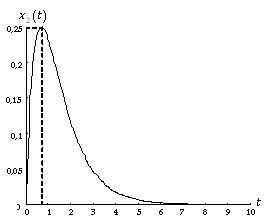 |
Figura 2.11. Respuesta temporal de las variables de estado para ![\[{x_1}\left( 0 \right) = {x_2}\left( 0 \right) = 0{\rm{ y }}u\left( t \right) = 1\left( t \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-52-c.png) . . |
|
Con lo cual la ecuación (2.87) se escribirá de la forma
![\[\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {2{e^{ - t}} - {e^{ - 2t}}} & {{e^{ - t}} - {e^{ - 2t}}} \\ { - 2{e^{ - t}} + 2{e^{ - 2t}}} & { - {e^{ - t}} + 2{e^{ - 2t}}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}\left( 0 \right)} \\ {{x_2}\left( 0 \right)} \\ \end{array}} \right) + \left( {\begin{array}{*{20}{c}} { - {e^{ - t}} + {\textstyle{1 \over 2}}{e^{ - 2t}} + {\textstyle{1 \over 2}}} \\ {{e^{ - t}} - {e^{ - 2t}}} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-53%282.89%29.png) |
(2.89) |
La expresión anterior es la solución completa al comportamiento dinámico del sistema cuando la entrada es una señal escalón unitario. Por tanto, para conocer el estado del sistema en un instante de tiempo t, sólo hay que sustituir en la ecuación el valor de ese tiempo junto a las condiciones iniciales. Así por ejemplo, si el estado inicial es cero, la respuesta del sistema (trayectoria del vector de estado) es
![\[\left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)} \\ {{x_2}\left( t \right)} \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - {e^{ - t}} + {\textstyle{1 \over 2}}{e^{ - 2t}} + {\textstyle{1 \over 2}}} \\ {{e^{ - t}} - {e^{ - 2t}}} \\ \end{array}} \right)\]](/antonio.barragan/files/archivos_usuarios/78/form2.4-54%282.90%29.png) |
(2.90) |
El la figura 2.11 se muestra la evolución temporal del vector de estado según la ecuación (2.90). A modo de conclusión, en este ejemplo se ha mostrado como mediante la ecuación general (2.73), que implica el cálculo previo de la matriz de transición de estado17, se puede calcular la respuesta temporal completa de un sistema (respuesta natural o no forzada más respuesta forzada) y, por ende, conocer su estado en cualquier instante t. Aunque su aplicación se limita a los sistemas lineales, esta metodología constituye una herramienta poderosa y fácil de escribir en forma de algoritmo para ser ejecutada en un computador.
 Versión para imprimir
Versión para imprimir- Inicie sesión para enviar comentarios





