![]()
Introducción a la Programación Funcional
![]()
1
Características de los lenguajes funcionales2
Comparativa entre lenguajes lógicos, funcionales e imperativos3
Definición y tipo de funciones4
Operaciones entre funcionesCaracterísticas de los lenguajes funcionales
Los lenguajes funcionales se basan en el concepto de función, por tanto, el objeto básico y fundamental que manejamos son las funciones, que se pueden considerar las principales estructuras de control en este tipo de lenguajes.
La base fundamental para comprender este tipo de lenguajes consiste en ver los programas y aplicaciones expresados a través de funciones y aplicación entre funciones.
Las características fundamentales de estos lenguajes se exponen a continuación:
Vistas las características fundamentales de los lenguajes funcionales, estos pueden clasificarse en dos tipos:
Comparativa entre lenguajes lógicos, funcionales e imperativos
Frente a los lenguajes declarativos e imperativos, los lenguajes funcionales ofrecen una serie de ventajas y de limitaciones.
VENTAJAS
LIMITACIONES
Definición y tipo de funciones
FUNCIONES
Las funciones establecen relaciones entre dos conjuntos, imponiendo la restricción única de que un elemento no puede tener dos imágenes, (ver Figura 1).
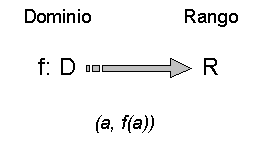
Definición de una función. Equivalente a f={(a,f(a))/a
Î D}Podemos definir una función por extensión o por comprensión. En el primer caso, la función se define indicando todos los pares (a, f(a)). En el segundo caso, la función se define mediante la indicación de una regla para calcular la imagen sobre el elemento del dominio.
|
|
Ejemplo de lista definida por extensión |
|
par={(1,false), (2,true), (3,false), (4,true), (5,false), (6,true), (7,false)...} doble={(0,0), (1,2), (2,4)...} |
|
|
|
Ejemplo de lista definida por comprensión |
|
par x=x mod 2==0 doble x=2*x |
|
Se dice que dos funciones son equivalentes si tienen el mismo conjunto de pares. Además hemos de tener en cuenta que el valor de una variable nunca cambia.
FUNCIONES PARCIALES
Son aquellas en las que la imagen de, al menos, un elemento no está definida.
|
|
Ejemplo de una función parcial |
|
Division x y (Ya que la operación de división por 0 no está definida). |
|
FUNCIONES TOTALES
Son aquellas en las que todos los elementos del dominio tienen definida una imagen.
Se puede realizar el cambio de función parcial a función total utilizando un elemento "indefinido" (o bottom). Este elemento nos sirve para conocer que elementos del dominio están indefinidos y realizar un adecuado control de errores en nuestros programas.
|
|
Ejemplo de función total obtenida a partir de una función parcial |
|
Division x y Division 5 0 = 1 |
|
En muchos casos, resulta interesante realizar operaciones con funciones. Podemos aplicar, sencillamente, una función sobre un elemento del dominio para obtener su imagen. Por ejemplo, dada la función f(x,y)=x+y, podemos aplicar f(2,3) para obtener como resultado 5.
También podemos realizar otros tipos de operaciones más complicadas entre funciones, por ejemplo la composición de funciones que consiste en que el resultado de una función se puede usar como argumento para otra función. Por ejemplo, si tenemos la función par(x), y la función doble(y), par(doble(7)) devolverá como resultado true.