
Práctica 5: Velocidad límite. Viscosidad de un fluido.
- 1 | Introducción y fundamento teórico
- 2 | Materiales y realización
- 3 | Resultados, discusión y cuestiones

5.6 Resultados y discusión
El alumno realizará una tabla con los valores de posición y tiempo obtenidos en el experimento. Los valores de dicha tabla se utilizarán para calcular la media de los tiempos para cada cada uno de los puntos de referencia. Una vez calculadas estas medias se representará directamente posición frente a tiempo en un sistema de ejes coordenados. Dicha representación permitirá determinar para el líquido problema en qué región el móvil se halla en el régimen de velocidad constante.
Una vez determinados los puntos en los que el móvil se mueve con velocidad constante, el alumno realizará una regresión lineal ajustando una recta a estos puntos (caso de haber más de dos; de haber solo dos se determinará la pendiente a partir directamente de los puntos).
La velocidad límite se obtendrá como resultado de esta
regresión lineal y, usando la ecuación (5.7), se
deducirá el valor del coeficiente de viscosidad,  , y su error
experimental. También se discutirán las posibles fuentes de error
en el procedimiento
descrito para la medición empírica del coeficiente de viscosidad.
, y su error
experimental. También se discutirán las posibles fuentes de error
en el procedimiento
descrito para la medición empírica del coeficiente de viscosidad.
5.7 Cuestiones propuestas
Cuestión 1
Según lo aprendido en la presente práctica, ¿será diferente la velocidad de dos gotas de lluvia que caen desde nubes a diferente altura? ¿Por qué?
Cuestión 2
A partir de la expresión de la velocidad límite en caída libre (5.7), ¿qué se corrige con un paracaídas para evitar una caída fatal?.
Cuestión 3
Resolvamos una "vieja" cuestión: si lanzamos desde suficiente altura dos esferas macizas de igual radio, la primera de hierro y la segunda de un material tres veces más denso: ¿cuál caerá antes y con mayor velocidad? ¿Y si las dos esferas en vez de idéntico radio tienen la misma masa?.
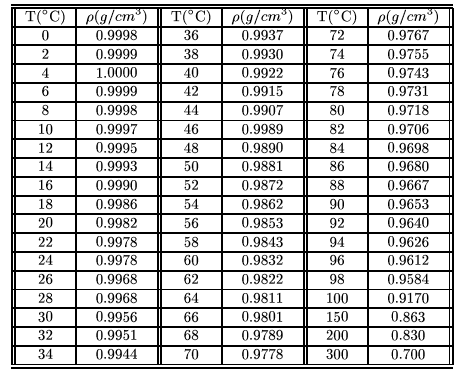
Cuadro 5.1 - Densidad del agua en función de la temperatura
Cuadro 5.2 - Datos experimentales de la práctica para el cálculo de la viscosidad de un líquido








